数日前の日記の中で、「緯度1度あたりの長さは、緯度の高低に依らず一定と予想して、MySQLで計算してみたところ、差が出てびっくり」という実験結果を紹介しました。
http://sakaik.hateblo.jp/entry/20191202/mysql_gis_metre_per_degree
これは、地球が(そして今回計算に使用した JGD2011が)真球ではなく回転楕円体だからということに起因するものであると、すぐに想像できましたが、いやまて、よく見ると高緯度のほうが1度あたりの距離が長い。
mysql> SELECT id, ST_Distance(pos1, pos2) FROM g3 ORDER BY ID; +------+-------------------------+ | id | ST_Distance(pos1, pos2) | +------+-------------------------+ | 0 | 110573.13812416371 | | 10 | 110610.23595555034 | | 20 | 110710.37167306663 | | 30 | 110861.46743133431 | | 35 | 110950.61420268985 | | 40 | 111045.29885197058 | | 50 | 111239.69315258414 | | 60 | 111421.20351156592 | | 70 | 111567.93710081652 | | 80 | 111662.1956839133 | | 90 | 111692.61028462648 | +------+-------------------------+
地球楕円体(赤道方向のほうが極方向よりも長い回転楕円体)は、赤道付近の半径が真球の場合に比べて伸びているのだから、普通に考えれば低緯度(赤道に近いほう)が1度あたりの距離は長くなるはず。 なのに、緯度0度よりも90度に近くなるに従って1度あたりの距離が長くなっているのは、直観に反する! というのが前回の日記での疑問でした。
なぜそう思ったのか
イメージが掴みやすいように、扁平率を思いっきり大きくした以下のような楕円を地球だと考えてみます。この地球上に点Aと点Bがあるときを考えます。
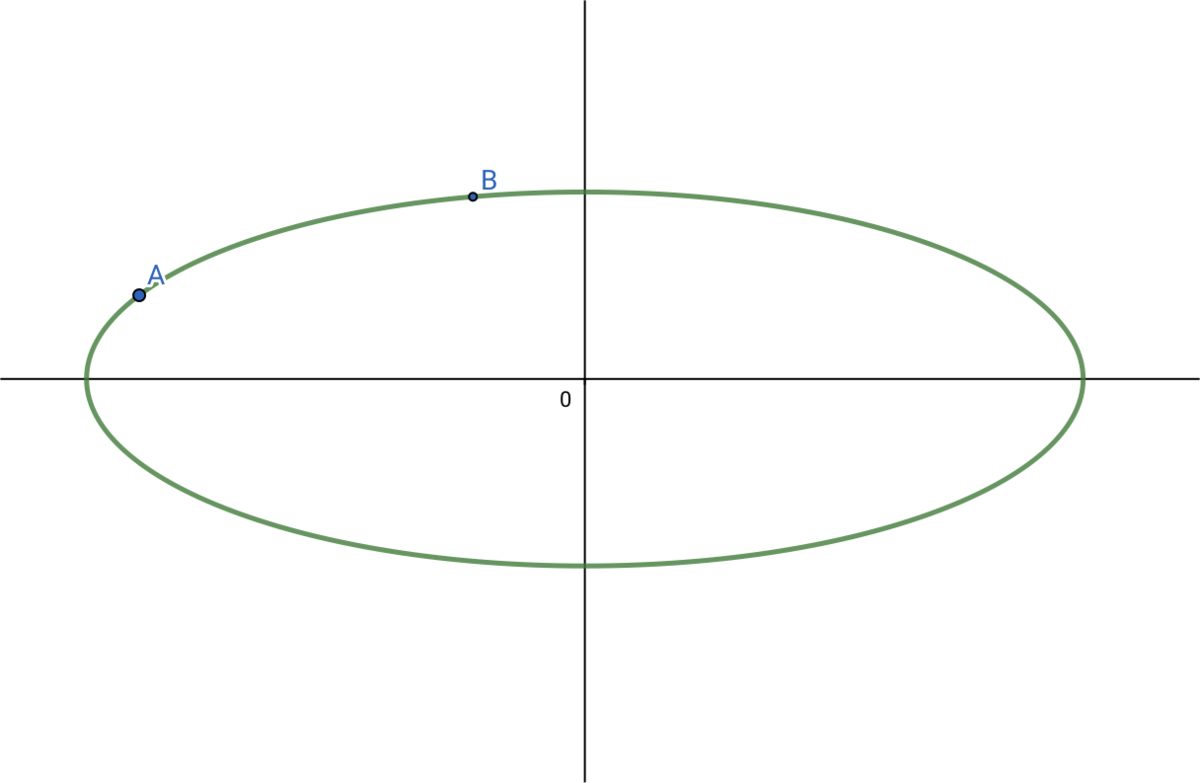
以下のように、点A、点Bそれぞれに地球の中心から線をひっぱります。
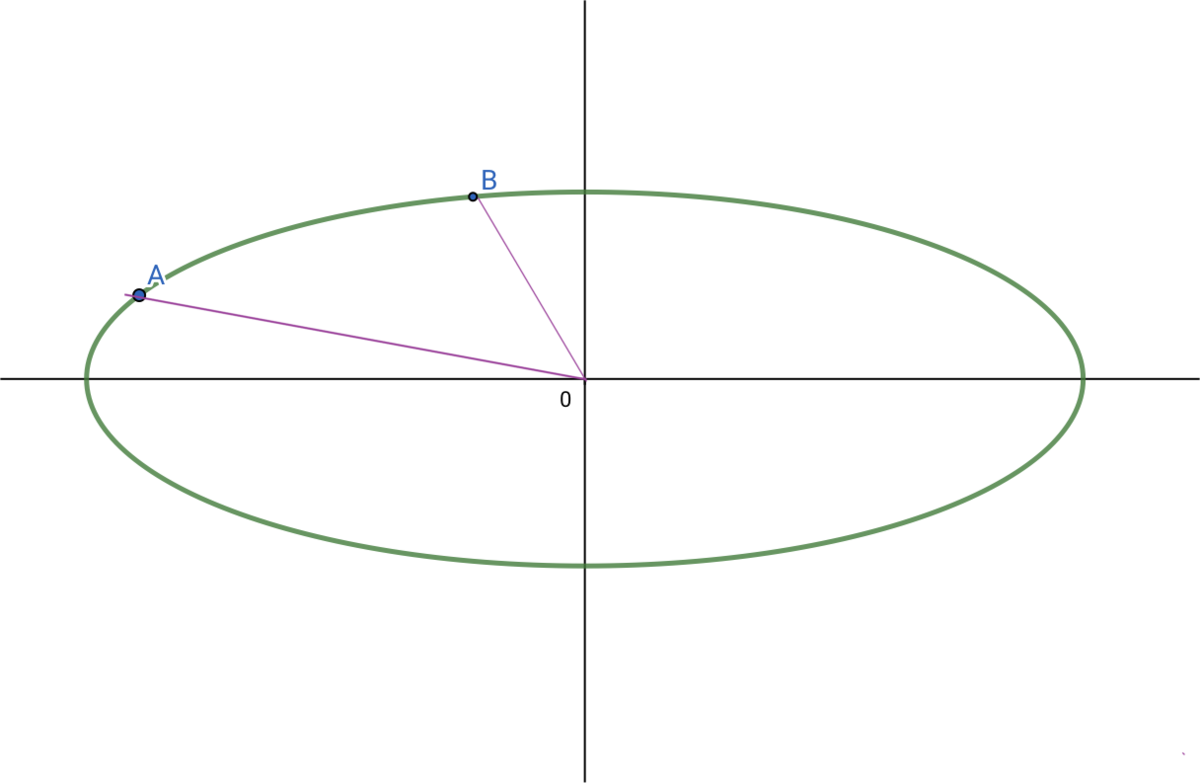
このとき、これらの線が長軸となす角度を、緯度と考えました。
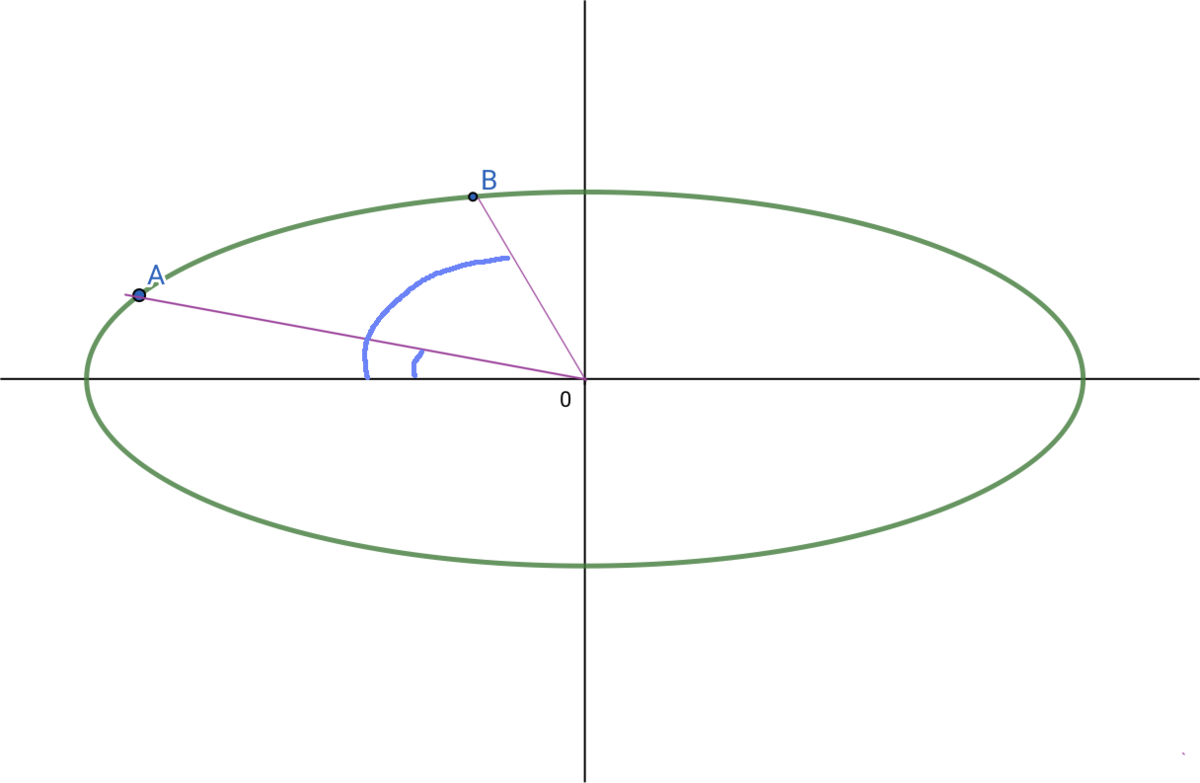
つまりこのとき、点A付近(低緯度)付近の1度と、点B付近(高緯度)付近の1度を比べると、明らかに点A付近のほうが長くなります。MySQLで計算した結果の値と逆の感覚です。「明らかに」の部分がピンと来ない人は、中心の角度を45度にした線を描いてみて、赤道~45度の弧の長さと、45度~90度の弧の長さを比較してみると良いでしょう。MySQLの結果の値自体が誤っているわけではないことは、他のソースで確認済なので、「明らかに」感じたほうが誤っているとしか考えようがありません。何がおかしいのでしょうか。
ほんとの緯度の定義
実は「緯度」の定義が、上で書いたようなものとは異なっていることがわかりました。 これがわかったのは高校の教科書のおかげです。高校の教科書、すごい!
元はと言えば、先日のセミナーで「ベッセル楕円体って中学あたりで習ったよね」と発言してしまったことが、どうも庶民感覚(笑)とずれていたらしいと知ったことで、教科書を取り扱っている本屋さんに中高の地学の教科書を確認しに行ったのですが、まぁこの話自体は「高校で、地球の形について習う。回転楕円体(出版社によっては地球楕円体)という用語はあるが、GRS80については出て来ない」というのが結論でした。 これを確認している際、あるひとつの教科書(出版社名失念)で、緯度の定義についてさらりと触れられていたのです。教科書、すごい!
まず、観測点Aにおける楕円体の接線を考えます。
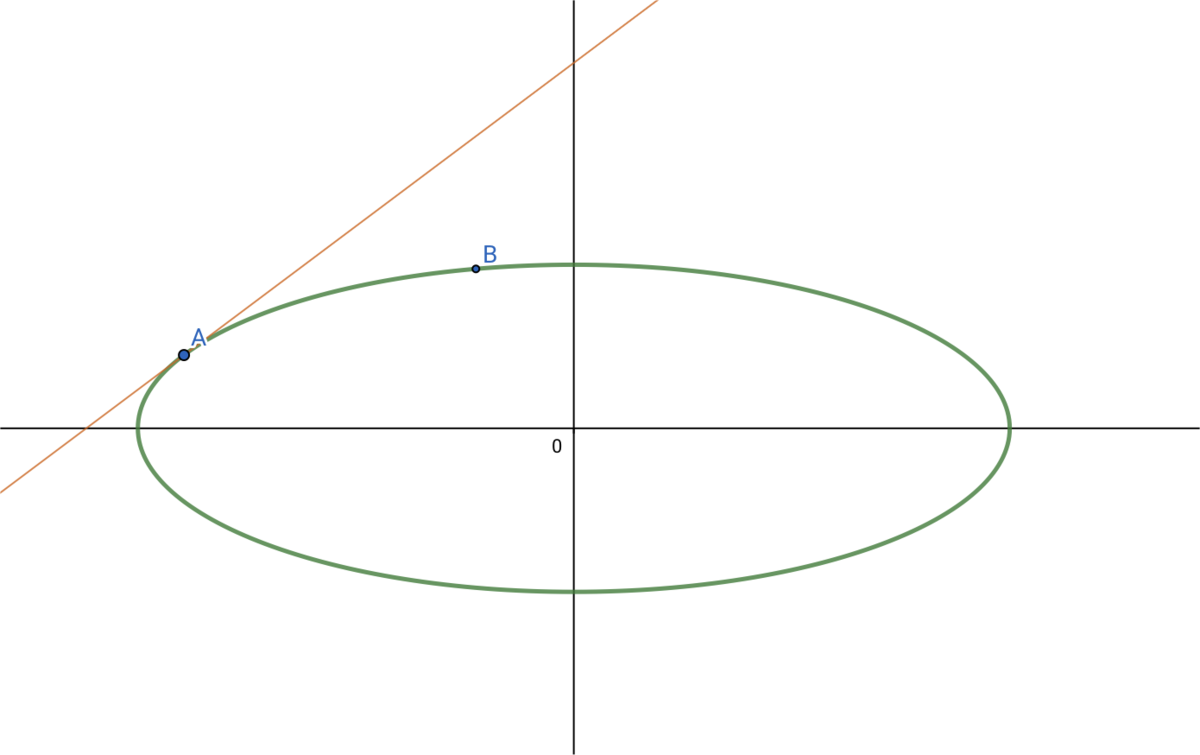
その接線に直交する線を引きます(=観測点における鉛直方向)
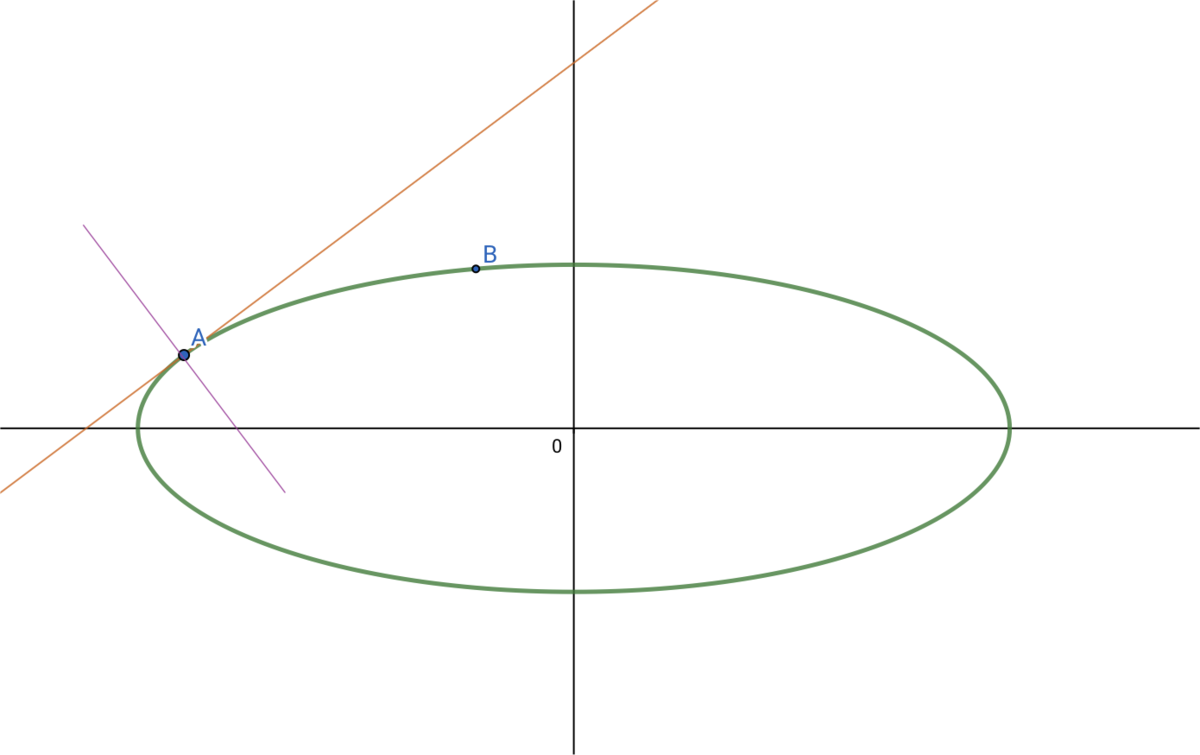
その線が長軸と交わるところの角度、これが「緯度」なのです。
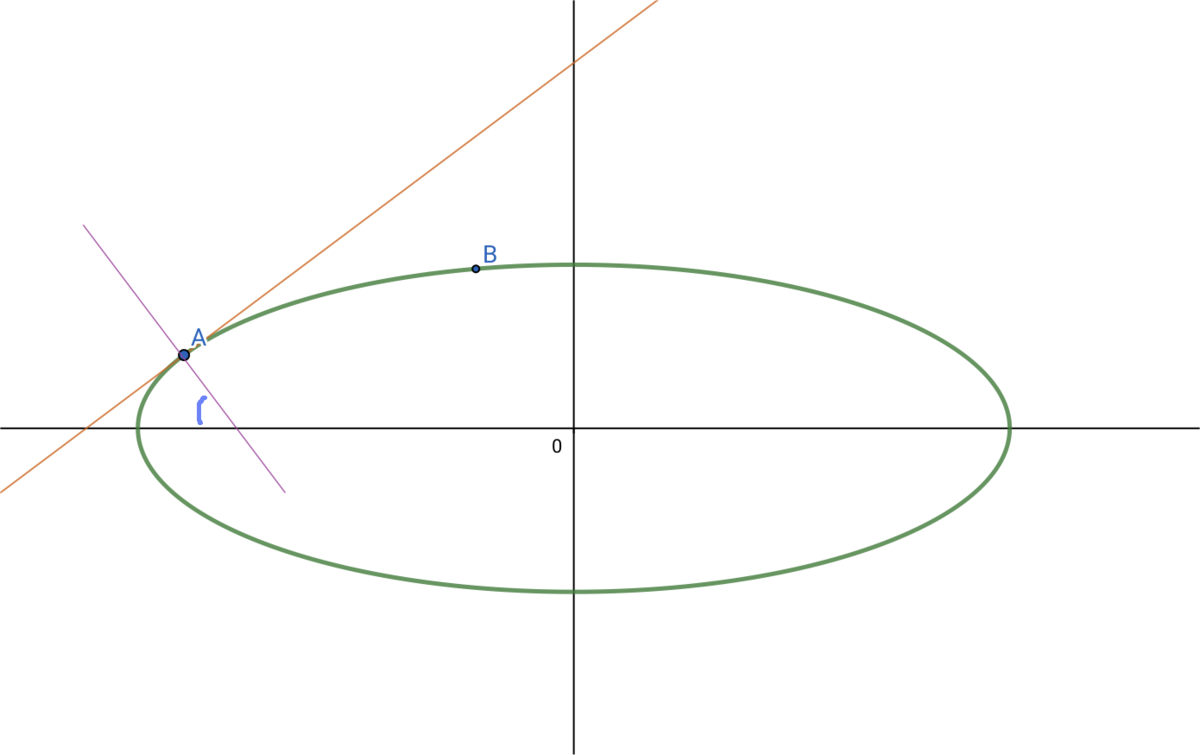
考えてみれば人工衛星による観測のない時代、「真下」を知る根拠は重力なわけで、その「真下」は必ずしも地球中心を向いていない。なお、地球回転による遠心力もあるので、更にすこしずれるらしいですが、遠心力の影響は重力の力に比べてかなり小さいそうです。
参考までに点Bにおける鉛直方向の図も示しておきます。
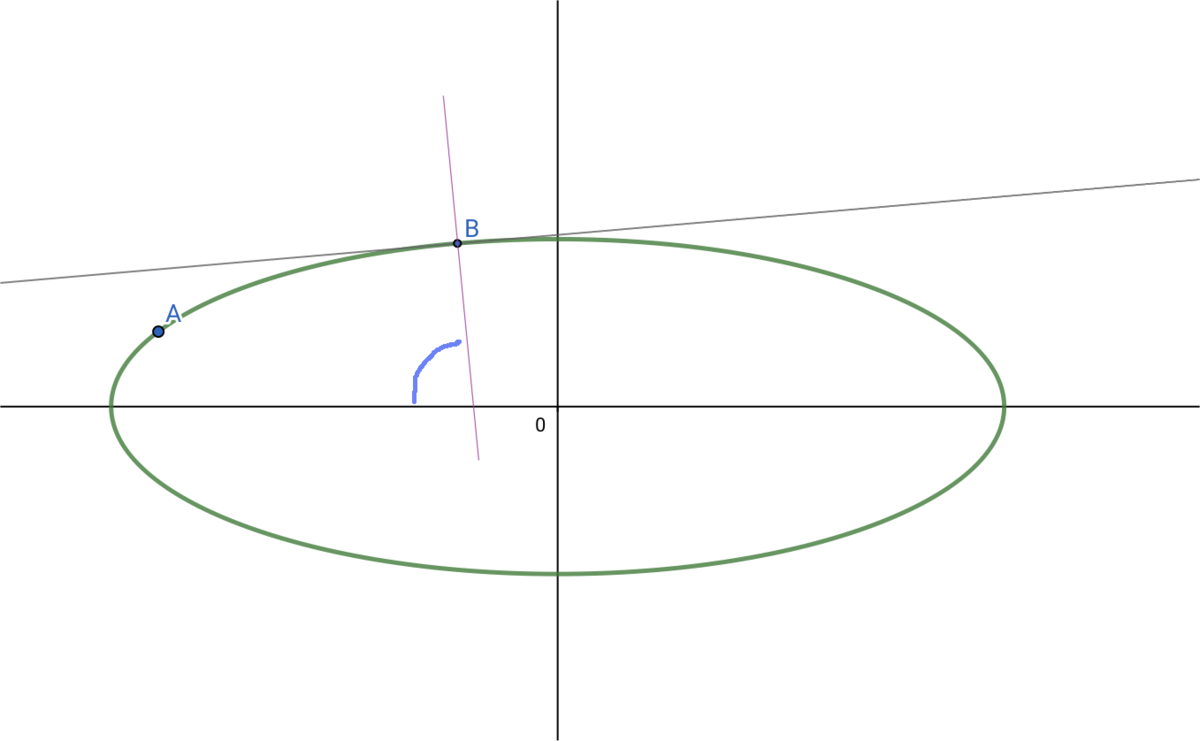
これらの図を見てみると、高緯度における1度のほうが距離が長くなるのも納得できますね。実際の地球は扁平率が 298分の1程度なのでその差は微々たるものですが、それでも緯度10度隔てると1度あたりの距離は100m(0.1%ほど)くらい差がでるようです。
そもそもの歴史的な話として
そもそもが、高緯度における1度の長さを測ろうとしていた人たちがいて、どうも思っていたのよりも大きくなる。なんでだ?と疑問に思ったところから、地球が回転楕円体である(真球ではない)と気づいたということのようで、なるほど勉強になります。地球の形、奥が深い!
(2019/12/14追記) "ほんとの定義" などない!
「ほんとの緯度の定義」と私が書いた点に対して、ご指摘をいただきました。
ほんとの定義というより、(普段注釈なしで使っている「緯度」は)地理緯度を指していて、その地理緯度の定義ですね。当初の説明は地心緯度。このへんは Wikipedia:緯度 参照 https://t.co/NL1n4TcsmS
— とーか (arita) (@tohka383) 2019年12月12日
JGD2011とかWGS84とかを見ている上では、緯度の定義は上に書いたとおりということで間違いはないのですが、これが「緯度の本当の定義」と呼ぶのは、言い過ぎだったようです。今回結論とした緯度の定義は「地理緯度」(地理座標系での緯度ってことですかね)であり、これとは別に、ちゃんと「地心緯度」というものもあるとのこと(この日記の冒頭で「こうだと思っていたんですが」と書いたほう)。
ご指摘いただきありがとうございました。 不正確なことを書いちゃったけど、こうやって指摘いただけた時、あぁ書いてよかったなぁと思います。ひとつ賢くなった^^
(2021/07/10追記) 地心緯度と測地緯度
ちょうどいま読んでいた本に、地心緯度と測地緯度についての言及が出てきて、「あ、これだ」とこの記事を思い出したので追記しておきます。
地心緯度:楕円体の中心を基準とする緯度
測地緯度:楕円体面の法線が赤道面となす確度
とのことで(久保信明著 『図解よくわかる 衛星測位と位置情報』4章28)、地上にいるときは測地緯度が自然に感じるけど、確かにGNSSだと地心緯度が自然だよなと感じました。
